
A cura della docente Stefania Donadio e della classe 3D a.s. 2014/15 – Scuola secondaria di I grado “Don Milani” di Genova”.
Le difficoltà concettuali incontrate nello studio della matematica sono da sempre al centro della ricerca didattica, specialmente in quegli apprendimenti che permettono di avviare al pensiero teorico. Questo tema assume una certa rilevanza perché saper utilizzare le definizioni, produrre formalizzazioni e argomentazioni sono alcuni dei traguardi per lo sviluppo delle competenze di matematica individuati nelle Indicazioni Nazionali per il curricolo della scuola del primo ciclo.
Nella panoramica degli strumenti utili a realizzare esperienze didattiche significative per condurre gli alunni a raggiungere i concetti teorici con consapevolezza, gli insegnanti possono trovare un valido alleato nelle TIC.
Questa che segue, è la descrizione di un laboratorio per l’avvio alle definizioni in geometria.
Gli strumenti utilizzati sono gratuiti e disponibili in rete: PbWorks[1], un ambiente online di lavoro che fornisce file wiki, una chat di discussione, l’organizzazione in cartelle per caricare, condividere, archiviare, modificare i documenti; e Geogebra[2], un software open-source di geometria dinamica molto intuitivo e ricco di strumenti per agevolare l’esplorazione diretta degli oggetti matematici, per usare in modo integrato diverse rappresentazioni e linguaggi (grafico, algebrico, numerico) e con molte altre potenzialità.
L’ambiente di lavoro online, grazie agli strumenti per la scrittura condivisa, consente di realizzare la socializzazione delle conoscenze, mediata dal computer, e l’apprendimento collaborativo. Il software di geometria dinamica permette di mettere in crisi la rappresentazione stereotipata delle figure e facilita l’elaborazione di nuovi schemi, in un’impostazione didattica rivolta al problem solving.
Il laboratorio è svolto in una classe prima della scuola secondaria di I grado “Don Milani” di Genova e si sviluppa partendo da una situazione di riferimento significativa, cioè già fissata nell’esperienza e nella memoria, la rappresentazione grafica di un quadrato con carta e matita, per poi riflettere sulla sua definizione e sulle proprietà che lo caratterizzano.
È un’attività breve, che a parere nostro ha senso proporre nel primo anno della scuola media nei casi in cui si vuole progettare un approccio graduale all’uso del computer e procedere su una buona base e con maggior respiro negli anni successivi, in quello che potrebbe essere un concreto investimento nelle tecnologie didattiche, ma può trovare collocazione anche negli anni successivi.
La consegna è stata la seguente: “Costruisci la figura, prima sul foglio con la matita e le attrezzature da disegno, poi con Geogebra, esplorando liberamente gli strumenti del software”.
Gli interventi dei ragazzi sono stati numerosi: riportiamo quelli più significativi per contenuti didattici e riflessioni metacognitive, alternandoli alle richieste della docente che ha condotto l’attività.
– Andrea (istruzioni per costruire un quadrato sul foglio): Per fare un quadrato devi prendere un foglio, possibilmente a quadretti 0,5 cm e un righello. Tracciare una retta ad es. di 2 cm chiusa da due punti, da uno dei due punti tracciare un’altra retta verso l’alto o verso il basso sempre di 2 cm e in cima mettere un altro punto. Da questo punto traccia un’altra retta di 2 cm verso destra o sinistra a seconda di dove era partita la linea verso l’alto e poi chiudi i due punti con un altro segmento di 2.
– Emir: anche sulla vista grafica di Geogebra sono partito dall’incrocio degli assi, ho fissato quattro punti contando i quadretti, senza preoccuparmi di altro.
Costruito il quadrato con il software, la richiesta successiva è stata di provare a spostarlo, trascinando i lati per verificare se si deforma. La libera esplorazione consente di scoprire la funzione di alcuni strumenti, ad esempio il trascinamento o la rotazione, che non servono – banalmente – a realizzare un disegno, ma a controllare la costruzione corretta di una figura. È bene confrontare nel gruppo i diversi protocolli di costruzione, per far sì che gli apprendimenti vengano socializzati.
– Noemy: Ho notato che ci sono diverse modi per costruire il quadrato. Posso partire da un segmento e poi portare la stessa lunghezza sugli altri lati e poi li faccio diventare perpendicolari, oppure prima posso prendere i segmenti perpendicolari e poi li modifico finché non sono uguali.
– Nathalie: il mio quadrato prima è diventato un trapezio, poi una specie di rombo e poi un quadrilatero strano.
Quest’ultimo intervento merita un’ulteriore riflessione, perché può rappresentare lo spunto che consente di passare da un caso specifico a una classe di oggetti matematici; l’insegnante interviene per focalizzare quali sono le proprietà che caratterizzano una figura e quelle che la definiscono.
– Professoressa: Perché i quadrati si deformano? Proviamo a rifare la figura, tenendo conto delle proprietà del quadrato, per esempio la perpendicolarità dei lati e la loro congruenza.
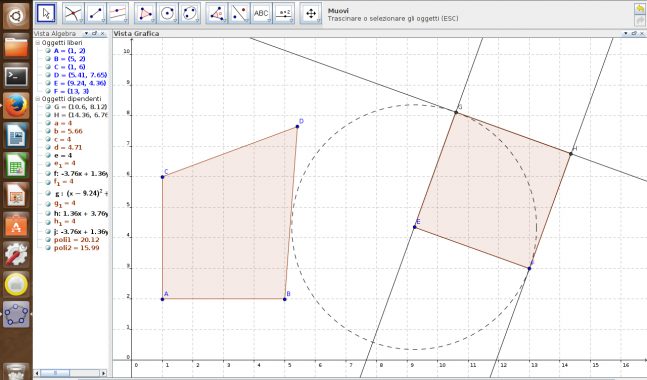
– Emanuele: I quadrati si deformano perché non hanno le giuste proprietà, quelle che li definiscono. Sono falsi quadrati, sono quadrati solo apparenti. Quelli veri devono restare quadrati anche se li sposti o indipendentemente da come li guardi.
Figura: a sinistra, un “falso quadrato” che si deforma col trascinamento; a destra un “quadrato vero” correttamente costruito.
Confrontare le costruzioni fatte con matita e righello con quelle realizzate con il software è un’attività molto utile, perché induce i ragazzi a riflettere sulle loro procedure convenzionali e quindi a ragionare. Parallelamente, gli alunni intuiscono l’importanza di una protocollo rigoroso di costruzione e l’uso di un linguaggio disambiguo e tecnico: nello scorrere delle attività, si nota lo sforzo di una descrizione via via più accurata e con l’uso di simboli.
– Marta (istruzioni per costruire un quadrato col software): Segno un punto chiamato A, segno un secondo punto B, dopo aver cliccato la voce del segmento, clicco sul punto A e porto la freccia sull’altro punto, il segmento si chiamerà a. Clicco sull’icona delle rette e vado sulla voce “retta perpendicolare” e clicco il punto B e il segmento a. La retta si chiamerà b. Dopo aver costruito la retta b, ne costruisco un’altra allo stesso modo, questa si chiamerà c. Ne costruisco poi un’altra allo stesso modo, cliccando sulla retta c e otterrò la retta che si chiamerà d. Fatto questo, clicco l’icona con i punti e la voce “punto d’incontro” e clicco i due punti d’incontro trovati dalle rette. Clicco l’icona per misurare le lunghezze, trascino orizzontalmente il punto B fino a far diventare il segmento AB della misura che voglio. Ripeto questa operazione anche per gli altri punti fino a quando tutti i segmenti sono della stessa lunghezza. Clicco sull’icona per misurare gli angoli e controllo se tutti gli angoli sono di 90°.
E finalmente si arriva al punto decisivo, la riflessione metadidattica sul significato di tutti questi tentativi. Il dibattito online si accende:
– Seth: ho capito che la prima costruzione che abbiamo fatto non è corretta, ma non so spiegare come mai se funziona sulla carta non funziona in Geogebra.
– Professoressa: Perché quello che funziona sul foglio non funziona col software?
– Sofia: forse perché io so cos’è un quadrato e quando lo disegno sul foglio non mi devo preoccupare di controllare tutte le sue proprietà. A Geogebra, invece, devo dire cos’è un quadrato perché non lo sa.
– Marco: Quando disegno un quadrato non penso a tutte le sue proprietà, lo faccio e basta, invece a Geogebra devo spiegare tutti i passaggi perché me lo disegna lui.
Spunti interessanti, subito rilanciati dal docente per stimolare altre riflessioni.
– Professoressa: Secondo voi a cosa è servito questo lavoro?
– Anthony: mi sono stupito di quanti strumenti servono per fare un quadrato: non solo punti e segmenti, ma il compasso, le rette perpendicolari da dove prendere i segmenti, i righelli per fare la lunghezza uguale, i goniometri per controllare.
– Ludovica: io ho capito che il PC non fa quello che faremmo noi, ma fa quello che gli diciamo e per questo dobbiamo imparare un linguaggio preciso per avere dal PC quello che ci occorre.
– Adriele: Con Geogebra abbiamo costruito un quadrilatero. Partendo da esso abbiamo costruito un quadrato controllando che ogni angolo misurasse 90° e guardando che ogni lato fosse della stessa misura: le istruzioni per creare un quadrato le abbiamo prima cercate noi, poi le abbiamo discusse insieme. Questo lavoro l’abbiamo fatto prima sul quaderno e secondo me la prof ce l’ha fatto fare per cominciare a prendere confidenza con il programma e per ripassare cosa significa il quadrato.
Alcune considerazioni conclusive: in questo laboratorio sono emerse riflessioni profonde e precoci per l’età degli alunni, che avevano già utilizzato l’ambiente di lavoro online, ma si sono confrontati per la prima volta con un software di geometria.
Il wiki per la scrittura condivisa permette di riportare in tempo reale tutti gli interventi, in modo che i ragazzi possano partecipare alla discussione collettiva e, in una fase successiva, confrontare le conclusioni provvisorie con le congetture iniziali o con le inferenze di metà percorso. L’insegnante può analizzare le affermazioni degli alunni per avere indicazioni sul loro ragionamento e restituire le proprie considerazioni.
Dal punto di vista disciplinare, la presenza di elementi legati alla percezione e alla esperienza diretta accanto ad attività di astrazione e generalizzazione, permettono l’avvio al pensiero teorico. Come anche l’uso di strumenti che permettono il confronto tra rappresentazioni diverse, ad esempio nel passaggio dal disegno alla verbalizzazione.
Spunta, infine, nella discussione tra pari la consapevolezza della necessità delle definizioni per motivi pratici e immediati: per non confondere il quadrato con gli altri quadrilateri, oppure per far sì che il computer esegua correttamente un disegno o una qualunque istruzione data.
(a cura della docente Stefania Donadio e della classe 3D a.s. 2014/15 – Scuola secondaria di I grado “Don Milani” di Genova)
[1] http://pbworks.com
[2] http://www.geogebra.org

Registrati a tuttoscuola

Benvenuto su Tuttoscuola.com!

Registrati a tuttoscuola
Grazie per esserti registrato
controlla il tuo indirizzo di posta per attivare il tuo abbonamento
